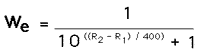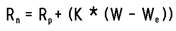1. ASL Player Ratings: ELO Rating Theory
ASL Player Ratings use the ELO rating methodology as implemented by Bruno Nitrosso on his Area site (see: asl-area.org). The following is an edited and updated version of Bruno's description of the ELO rating system.
Developed by Arpad Elo in the early 1960's, ELO is based on a probabilistic approach. The idea is that a more skilled player will have a higher probability of beating a less skilled one and ratings reflect that probability. Player X's rating would then be representative of how likely it is he or she would beat another player Y who has another given rating. This specific probability of winning is calculated using the formula below:
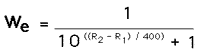
We is the specific win-expectancy (probability), R1 is the players current rating, and R2 the opponents current rating. In our previous X against Y example, a value of 0.62 for We would mean X should beat Y 62 times out of a hundred.
If we have players X and Y play each other a hundred times and see that X beats Y 58 times, that could be indicative that their rating difference is a bit too high and we'd rather adjust them. How much? This is question 2.
Now, one could have them play only 10 times and, having X score 6 wins (instead of 6.2 !), decide to update the ratings accordingly.
One could even have them play just once and, having X win 1 (instead of 0.62 !), decide to update the ratings.
So this is question 1 : how often do we adjust ratings? And assuming you do decide to upgrade ratings after a series of wins : how much would you upgrade them? If the former rating difference corresponded to a 0.62 while the recent series implies a 0.7 : would you ignore the former history and only stick to the recent one?
So question 2 is : how much weight are we to give to former games and new games?
Question 1 : How often to update ratings
In AREA, and now ASL Player Ratings, ratings are updated once a day. A typical tournament day will see people playing 2 or 3 games, but sometimes it maybe only 1 and sometimes 5.
Question 2 : How much to update ratings
If a rating difference between X and Y gives a We of 62%, based on a series of 40+ games each, and after playing 2 games X wins both games... does this mean the "correct" rating difference is the one that leads to 100% victories? Or 67%? Or what figure between the historical 62 and the marginal 100?
The way ELO works, there is a parameter, the K factor, that gives the inertia or resilience to ratings. Here is the formula:
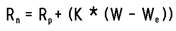
Rn is the players new rating, Rp is the players previous rating, W is the expectancy based on the new games, We is the previous win-expectancy based on the current ratings difference.
As for K, it is the factor that weights more or less the impact on ratings of the new games results. A high value would give a lot of importance to newest games, a low one would pretty much leave unchanged the ratings.
ASL Player Ratings uses different values for K depending on circumstances. Players with an evolving skill level have their rating move faster than players in a more mature stage by giving higher a K-factor to new players: the first 10 games count double, so to speak.
Another one, is to believe that players with a high rating achieve it after a large experience and are therefore, probably, at more mature stage. This is done by lowering the K-factor for players with higher ratings (see Table below).
| Rating |
K-Value |
| 0 .. 1800 | 40 |
| 1800 .. 2000 | 30 |
| 2000 .. 2200 | 20 |
| 2200+ | 10 |
Methodology Updates: Several changes were implemented in October 2021:
Firstly, each players initial rating is now 1500. The original AREA had different starting positions (1650, 1500, 1400) for players based on ad hoc assessments at the time. Now that players have enough playing history, everyone starts from the same rating. For almost all players this produces a very minor rating change.
Secondly, a decay factor for players who have stopped playing for a long time has been introduced to make sure rankings are up-to-date and reflect current skills. Ratings begin to decline three years after their last tournament playing [at a rate of about 35 points per year] but are capped at a fraction (15%) of a player’s rating at the time decay came into effect. Thus, the effect is muted and concerns only players having stopped for a long time. The cap on the maximum total decay is based on the concept that players' skills, while slowly atrophying, never fall too far away from the last recorded rating. Decay factors are often found in ratings tools. It is hoped that this approach to skills' decay will be less opaque than others, which use very complex formulas hard for players to comprehend. It does raise again the question of whether to use another ratings tool such as Glicko in the future if there's a need for it.
Finally, game eligibility has been streamlined to include only competitive games played in real-time (whether FtF or VASL).
In combination, the impact is a very small decrease in ratings for most active players. This is primarily due to the decay factor, not so much due to the direct impact of decay, but because the ratings of some inactive opponents have decreased. Questions or comments always welcomed!
2. Top Fifteen Information
The Player Leaders section gathers additional dimensions to rank players. Most of these, such as ‘Games Played’, ‘Wins’, and ‘Tournament Wins’ are standard, absolute-value rankings.
One additional ranking, ‘Tournament Wins Score’ is based on a calculated rating for each player. It shows players with the strongest tournament performance rating, based on a weighted factor of tournament placings. Among competitive full ASL events involving games played in real time, players receive points for first, second and third place (in decreasing order). The number of points received also depends on the standing of each event based on the number of players participating. For example, a player winning a tournament where more than 64 players compete will receive 100 points, while a player finishing third at an event gathering 8 players will receive 4 points. Events with less than eight players receive a weight factor of zero.